|
G parity
In particle physics, G-parity is a multiplicative quantum number that results from the generalization of C-parity to multiplets of particles. ''C''-parity applies only to neutral systems; in the pion triplet, only π0 has ''C''-parity. On the other hand, strong interaction does not see electrical charge, so it cannot distinguish amongst π+, π0 and π−. We can generalize the ''C''-parity so it applies to all charge states of a given multiplet: :\mathcal G \begin \pi^+ \\ \pi^0 \\ \pi^- \end = \eta_G \begin \pi^+ \\ \pi^0 \\ \pi^- \end where ''ηG'' = ±1 are the eigenvalues of ''G''-parity. The ''G''-parity operator is defined as :\mathcal G = \mathcal C \, e^ where \mathcal C is the ''C''-parity operator, and ''I''2 is the operator associated with the 2nd component of the isospin "vector". ''G''-parity is a combination of charge conjugation and a π rad RAD or Rad may refer to: People * Robert Anthony Rad Dougall (born 1951), South African former racin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Physics
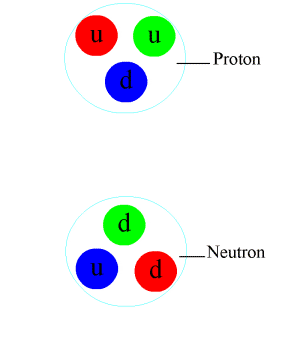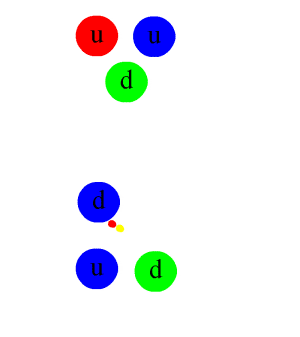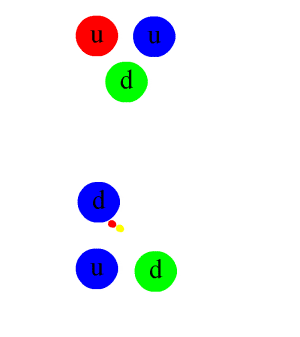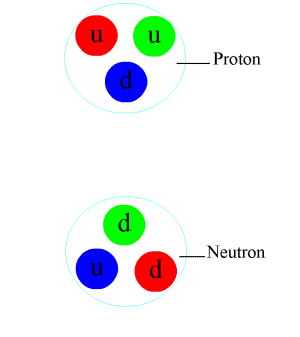
Particle physics or high energy physics is the study of fundamental particles and forces that constitute matter and radiation. The fundamental particles in the universe are classified in the Standard Model as fermions (matter particles) and bosons (force-carrying particles). There are three generations of fermions, but ordinary matter is made only from the first fermion generation. The first generation consists of up and down quarks which form protons and neutrons, and electrons and electron neutrinos. The three fundamental interactions known to be mediated by bosons are electromagnetism, the weak interaction, and the strong interaction. Quarks cannot exist on their own but form hadrons. Hadrons that contain an odd number of quarks are called baryons and those that contain an even number are called mesons. Two baryons, the proton and the neutron, make up most of the mass of ordinary matter. Mesons are unstable and the longest-lived last for only a few hundredths of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Quantum Number
In quantum field theory, multiplicative quantum numbers are conserved quantum numbers of a special kind. A given quantum number ''q'' is said to be additive if in a particle reaction the sum of the ''q''-values of the interacting particles is the same before and after the reaction. Most conserved quantum numbers are additive in this sense; the electric charge is one example. A multiplicative quantum number ''q'' is one for which the corresponding product, rather than the sum, is preserved. Any conserved quantum number is a symmetry of the Hamiltonian (quantum theory), Hamiltonian of the system (see Noether's theorem). Symmetry group (mathematics), groups which are examples of the abstract group called Z2 give rise to multiplicative quantum numbers. This group consists of an operation, P, whose square is the identity, P2 = 1. Thus, all symmetries which are mathematically similar to parity (physics) give rise to multiplicative quantum numbers. In principle, multiplicative quantum nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
C-parity
In physics, the C parity or charge parity is a multiplicative quantum number of some particles that describes their behavior under the symmetry operation of charge conjugation. Charge conjugation changes the sign of all quantum charges (that is, additive quantum numbers), including the electrical charge, baryon number and lepton number, and the flavor charges strangeness, charm, bottomness, topness and Isospin (''I''3). In contrast, it doesn't affect the mass, linear momentum or spin of a particle. Formalism Consider an operation \mathcal that transforms a particle into its antiparticle, :\mathcal C \, , \psi\rangle = , \bar \rangle. Both states must be normalizable, so that : 1 = \langle \psi , \psi \rangle = \langle \bar , \bar \rangle = \langle \psi , \mathcal^\dagger \mathcal C, \psi \rangle, which implies that \mathcal C is unitary, :\mathcal C \mathcal^\dagger =\mathbf. By acting on the particle twice with the \mathcal operator, : \mathcal^2 , \psi\rangle = \mathcal , \b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplet
In physics and particularly in particle physics, a multiplet is the state space for 'internal' degrees of freedom of a particle, that is, degrees of freedom associated to a particle itself, as opposed to 'external' degrees of freedom such as the particle's position in space. Examples of such degrees of freedom are the spin state of a particle in quantum mechanics, or the color, isospin and hypercharge state of particles in the Standard model of particle physics. Formally, we describe this state space by a vector space which carries the action of a group of continuous symmetries. Mathematical formulation Mathematically, multiplets are described via representations of a Lie group or its corresponding Lie algebra, and is usually used to refer to irreducible representations (irreps, for short). At the group level, this is a triplet (V,G,\rho) where * V is a vector space over a field (in the algebra sense) K, generally taken to be K = \mathbb or \mathbb * G is a Lie group. This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pion
In particle physics, a pion (or a pi meson, denoted with the Greek letter pi: ) is any of three subatomic particles: , , and . Each pion consists of a quark and an antiquark and is therefore a meson. Pions are the lightest mesons and, more generally, the lightest hadrons. They are unstable, with the charged pions and decaying after a mean lifetime of 26.033 nanoseconds ( seconds), and the neutral pion decaying after a much shorter lifetime of 85 attoseconds ( seconds). Charged pions most often decay into muons and muon neutrinos, while neutral pions generally decay into gamma rays. The exchange of virtual pions, along with vector, rho and omega mesons, provides an explanation for the residual strong force between nucleons. Pions are not produced in radioactive decay, but commonly are in high-energy collisions between hadrons. Pions also result from some matter–antimatter annihilation events. All types of pions are also produced in natural processes wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strong Interaction
The strong interaction or strong force is a fundamental interaction that confines quarks into proton, neutron, and other hadron particles. The strong interaction also binds neutrons and protons to create atomic nuclei, where it is called the nuclear force. Most of the mass of a common proton or neutron is the result of the strong interaction energy; the individual quarks provide only about 1% of the mass of a proton. At the range of 10−15 m (slightly more than the radius of a nucleon), the strong force is approximately 100 times as strong as electromagnetism, 106 times as strong as the weak interaction, and 1038 times as strong as gravitation. The strong interaction is observable at two ranges and mediated by two force carriers. On a larger scale (of about 1 to 3 femtometre, fm), it is the force (carried by mesons) that binds protons and neutrons (nucleons) together to form the atomic nucleus, nucleus of an atom. On the smaller scale (less than about 0.8 fm, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Charge
Electricity is the set of physical phenomena associated with the presence and motion of matter that has a property of electric charge. Electricity is related to magnetism, both being part of the phenomenon of electromagnetism, as described by Maxwell's equations. Various common phenomena are related to electricity, including lightning, static electricity, electric heating, electric discharges and many others. The presence of an electric charge, which can be either positive or negative, produces an electric field. The movement of electric charges is an electric current and produces a magnetic field. When a charge is placed in a location with a non-zero electric field, a force will act on it. The magnitude of this force is given by Coulomb's law. If the charge moves, the electric field would be doing work on the electric charge. Thus we can speak of electric potential at a certain point in space, which is equal to the work done by an external agent in carrying a unit of positiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isospin
In nuclear physics and particle physics, isospin (''I'') is a quantum number related to the up- and down quark content of the particle. More specifically, isospin symmetry is a subset of the flavour symmetry seen more broadly in the interactions of baryons and mesons. The name of the concept contains the term ''spin'' because its quantum mechanical description is mathematically similar to that of angular momentum (in particular, in the way it couples; for example, a proton–neutron pair can be coupled either in a state of total isospin 1 or in one of 0). But unlike angular momentum, it is a dimensionless quantity and is not actually any type of spin. Etymologically, the term was derived from isotopic spin, a confusing term to which nuclear physicists prefer isobaric spin, which is more precise in meaning. Before the concept of quarks was introduced, particles that are affected equally by the strong force but had different charges (e.g. protons and neutrons) were considered diff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charge Conjugation
In physics, charge conjugation is a transformation that switches all particles with their corresponding antiparticles, thus changing the sign of all charges: not only electric charge but also the charges relevant to other forces. The term C-symmetry is an abbreviation of the phrase "charge conjugation symmetry", and is used in discussions of the symmetry of physical laws under charge-conjugation. Other important discrete symmetries are P-symmetry (parity) and T-symmetry (time reversal). These discrete symmetries, C, P and T, are symmetries of the equations that describe the known fundamental forces of nature: electromagnetism, gravity, the strong and the weak interactions. Verifying whether some given mathematical equation correctly models nature requires giving physical interpretation not only to continuous symmetries, such as motion in time, but also to its discrete symmetries, and then determining whether nature adheres to these symmetries. Unlike the continuous symmetries, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that category was abolished in 1995). The radian is defined in the SI as being a dimensionless unit, with 1 rad = 1. Its symbol is accordingly often omitted, especially in mathematical writing. Definition One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle. More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, \theta = \frac, where is the subtended angle in radians, is arc length, and is radius. A right angle is exactly \frac radians. The rotation angle (360°) corresponding to one complete revolution is the length of the circumference divided by the radius, which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Baryon Number
In particle physics, the baryon number is a strictly conserved additive quantum number of a system. It is defined as ::B = \frac\left(n_\text - n_\bar\right), where ''n''q is the number of quarks, and ''n'' is the number of antiquarks. Baryons (three quarks) have a baryon number of +1, mesons (one quark, one antiquark) have a baryon number of 0, and antibaryons (three antiquarks) have a baryon number of −1. Exotic hadrons like pentaquarks (four quarks, one antiquark) and tetraquarks (two quarks, two antiquarks) are also classified as baryons and mesons depending on their baryon number. Baryon number vs. quark number Quarks carry not only electric charge, but also charges such as color charge and weak isospin. Because of a phenomenon known as ''color confinement'', a hadron cannot have a net color charge; that is, the total color charge of a particle has to be zero ("white"). A quark can have one of three "colors", dubbed "red", "green", and "blue"; while an antiquar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |